AI Concepts#
In this we are going to learn some AI concepts taking general and medical examples
Principle component Analysis#
# principle component analysis is all about preserving Variance as much as we can , because variance is informative
# Variance is how far a varible value is from mean of dataset, variables are features .. so we reduce the features by preserving variance
# eigen matrix (which has eigen values and eigen vectors) multiplied by X raw features = to get new features
# new features are not the subset of raw features
# lets understand by using iris dataset
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
iris = sns.load_dataset("iris")
iris.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
iris.describe()
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.057333 | 3.758000 | 1.199333 |
| std | 0.828066 | 0.435866 | 1.765298 | 0.762238 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 |
X = iris.iloc[:, 0:4]
print(X)
Y = iris.iloc[:, 4]
print(Y)
# Standardization , where mean = 0 and sd =1
iris_std = (X-X.mean())/ X.std()
print(iris_std)
# concatenate Y
iris_std = pd.concat([iris_std, Y], axis=1)
print(iris_std)
sepal_length sepal_width petal_length petal_width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
.. ... ... ... ...
145 6.7 3.0 5.2 2.3
146 6.3 2.5 5.0 1.9
147 6.5 3.0 5.2 2.0
148 6.2 3.4 5.4 2.3
149 5.9 3.0 5.1 1.8
[150 rows x 4 columns]
0 setosa
1 setosa
2 setosa
3 setosa
4 setosa
...
145 virginica
146 virginica
147 virginica
148 virginica
149 virginica
Name: species, Length: 150, dtype: object
sepal_length sepal_width petal_length petal_width
0 -0.897674 1.015602 -1.335752 -1.311052
1 -1.139200 -0.131539 -1.335752 -1.311052
2 -1.380727 0.327318 -1.392399 -1.311052
3 -1.501490 0.097889 -1.279104 -1.311052
4 -1.018437 1.245030 -1.335752 -1.311052
.. ... ... ... ...
145 1.034539 -0.131539 0.816859 1.443994
146 0.551486 -1.278680 0.703564 0.919223
147 0.793012 -0.131539 0.816859 1.050416
148 0.430722 0.786174 0.930154 1.443994
149 0.068433 -0.131539 0.760211 0.788031
[150 rows x 4 columns]
sepal_length sepal_width petal_length petal_width species
0 -0.897674 1.015602 -1.335752 -1.311052 setosa
1 -1.139200 -0.131539 -1.335752 -1.311052 setosa
2 -1.380727 0.327318 -1.392399 -1.311052 setosa
3 -1.501490 0.097889 -1.279104 -1.311052 setosa
4 -1.018437 1.245030 -1.335752 -1.311052 setosa
.. ... ... ... ... ...
145 1.034539 -0.131539 0.816859 1.443994 virginica
146 0.551486 -1.278680 0.703564 0.919223 virginica
147 0.793012 -0.131539 0.816859 1.050416 virginica
148 0.430722 0.786174 0.930154 1.443994 virginica
149 0.068433 -0.131539 0.760211 0.788031 virginica
[150 rows x 5 columns]
print(iris.describe())
print(iris_std.describe())
sepal_length sepal_width petal_length petal_width
count 150.000000 150.000000 150.000000 150.000000
mean 5.843333 3.057333 3.758000 1.199333
std 0.828066 0.435866 1.765298 0.762238
min 4.300000 2.000000 1.000000 0.100000
25% 5.100000 2.800000 1.600000 0.300000
50% 5.800000 3.000000 4.350000 1.300000
75% 6.400000 3.300000 5.100000 1.800000
max 7.900000 4.400000 6.900000 2.500000
sepal_length sepal_width petal_length petal_width
count 1.500000e+02 1.500000e+02 1.500000e+02 1.500000e+02
mean -5.684342e-16 -7.815970e-16 -2.842171e-16 -3.789561e-16
std 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
min -1.863780e+00 -2.425820e+00 -1.562342e+00 -1.442245e+00
25% -8.976739e-01 -5.903951e-01 -1.222456e+00 -1.179859e+00
50% -5.233076e-02 -1.315388e-01 3.353541e-01 1.320673e-01
75% 6.722490e-01 5.567457e-01 7.602115e-01 7.880307e-01
max 2.483699e+00 3.080455e+00 1.779869e+00 1.706379e+00
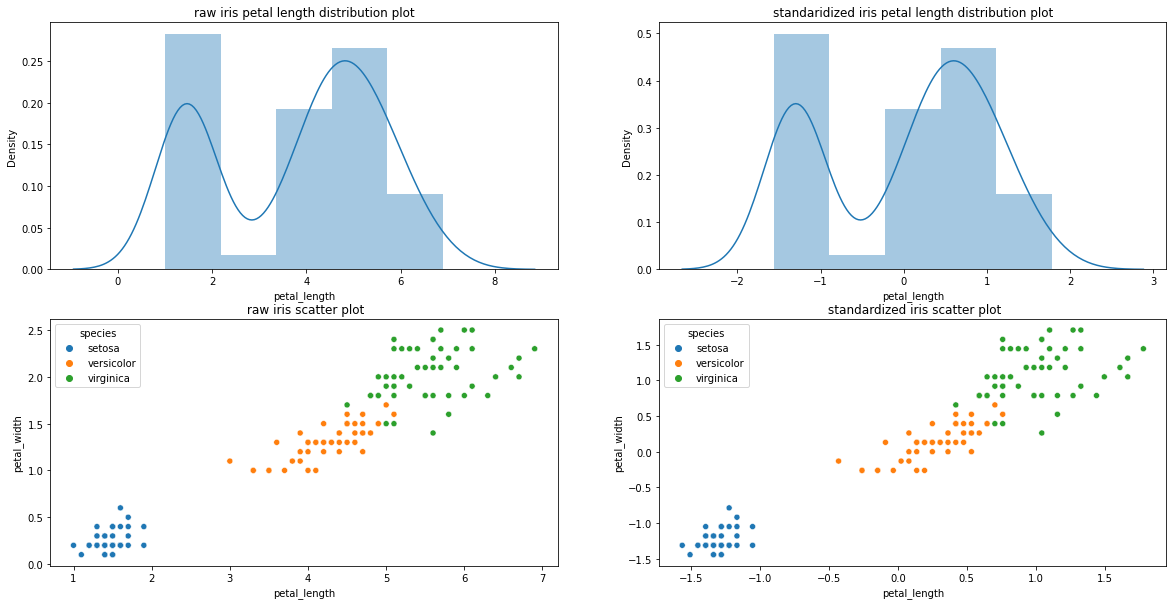
# Lets see by standaridization whether we preserved the information or variance by plotting
print("Plots showed distribution and scatter preserved , No change , where as data standardized at center zero" )
print("---------------------------------------------------------------------------------------------------------")
fig, axes = plt.subplots(nrows= 2, ncols= 2, figsize = (20, 10))
print(axes)
axes_0 = sns.distplot(iris['petal_length'], hist= True, kde= True, ax = axes[0,0])
axes_0.set_title("raw iris petal length distribution plot")
axes_1 = sns.distplot(iris_std['petal_length'], hist= True, kde= True, ax= axes[0,1])
axes_1.set_title("standaridized iris petal length distribution plot")
axes_2 = sns.scatterplot(x= "petal_length", y= "petal_width" , data= iris, hue= 'species', ax = axes[1,0])
axes_2.set_title(" raw iris scatter plot")
axes_2 = sns.scatterplot(x= "petal_length", y= "petal_width", data= iris_std, hue= 'species', ax = axes[1,1])
axes_2.set_title(" standardized iris scatter plot")
Plots showed distribution and scatter preserved , No change , where as data standardized at center zero
---------------------------------------------------------------------------------------------------------
[[<matplotlib.axes._subplots.AxesSubplot object at 0x7f3d5bf2ae50>
<matplotlib.axes._subplots.AxesSubplot object at 0x7f3d5be46790>]
[<matplotlib.axes._subplots.AxesSubplot object at 0x7f3d5bdfdd50>
<matplotlib.axes._subplots.AxesSubplot object at 0x7f3d5bdc3250>]]
/usr/local/lib/python3.7/dist-packages/seaborn/distributions.py:2619: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
warnings.warn(msg, FutureWarning)
/usr/local/lib/python3.7/dist-packages/seaborn/distributions.py:2619: FutureWarning: `distplot` is a deprecated function and will be removed in a future version. Please adapt your code to use either `displot` (a figure-level function with similar flexibility) or `histplot` (an axes-level function for histograms).
warnings.warn(msg, FutureWarning)
Text(0.5, 1.0, ' standardized iris scatter plot')
# Now data is standardized , next we can perform
# ---- preparing correlation matrix using numpy
#------ finding eigen vector and eigen values using matrix linalg.eig
# ----
X_std = iris_std.iloc[:, 0:4]
print(X_std)
y = iris_std.iloc[:,4]
print(y)
sepal_length sepal_width petal_length petal_width
0 -0.897674 1.015602 -1.335752 -1.311052
1 -1.139200 -0.131539 -1.335752 -1.311052
2 -1.380727 0.327318 -1.392399 -1.311052
3 -1.501490 0.097889 -1.279104 -1.311052
4 -1.018437 1.245030 -1.335752 -1.311052
.. ... ... ... ...
145 1.034539 -0.131539 0.816859 1.443994
146 0.551486 -1.278680 0.703564 0.919223
147 0.793012 -0.131539 0.816859 1.050416
148 0.430722 0.786174 0.930154 1.443994
149 0.068433 -0.131539 0.760211 0.788031
[150 rows x 4 columns]
0 setosa
1 setosa
2 setosa
3 setosa
4 setosa
...
145 virginica
146 virginica
147 virginica
148 virginica
149 virginica
Name: species, Length: 150, dtype: object
from sklearn.decomposition import PCA
sklearn_pca = PCA(n_components= 2, random_state= 100)
PCs = sklearn_pca.fit_transform(X_std)
print(PCs.shape)
print(X_std.shape)
print(PCs)
(150, 2)
(150, 4)
[[-2.25714118 0.47842383]
[-2.07401302 -0.67188269]
[-2.35633511 -0.34076642]
[-2.29170679 -0.59539986]
[-2.3818627 0.64467566]
[-2.06870061 1.4842053 ]
[-2.43586845 0.04748512]
[-2.22539189 0.222403 ]
[-2.32684533 -1.1116037 ]
[-2.17703491 -0.46744757]
[-2.15907699 1.04020587]
[-2.31836413 0.132634 ]
[-2.2110437 -0.72624318]
[-2.62430902 -0.95829635]
[-2.19139921 1.85384655]
[-2.25466121 2.67731523]
[-2.20021676 1.47865573]
[-2.18303613 0.48720613]
[-1.89223284 1.40032757]
[-2.33554476 1.1240836 ]
[-1.90793125 0.40749058]
[-2.19964383 0.92103587]
[-2.76508142 0.4568133 ]
[-1.81259716 0.08527285]
[-2.21972701 0.13679618]
[-1.9453293 -0.62352971]
[-2.04430277 0.24135499]
[-2.1613365 0.52538942]
[-2.13241965 0.312172 ]
[-2.25769799 -0.33660425]
[-2.13297647 -0.50285608]
[-1.82547925 0.42228039]
[-2.60621687 1.78758727]
[-2.43800983 2.1435468 ]
[-2.10292986 -0.45866527]
[-2.20043723 -0.20541922]
[-2.03831765 0.65934923]
[-2.51889339 0.59031516]
[-2.42152026 -0.90116107]
[-2.16246625 0.2679812 ]
[-2.27884081 0.44024054]
[-1.85191836 -2.32961074]
[-2.54511203 -0.47750102]
[-1.95788857 0.47074961]
[-2.12992356 1.13841546]
[-2.06283361 -0.70867859]
[-2.37677076 1.11668869]
[-2.38638171 -0.38495723]
[-2.22200263 0.99462767]
[-2.19647504 0.00918558]
[ 1.09810244 0.86009103]
[ 0.72889556 0.59262936]
[ 1.2368358 0.61423989]
[ 0.40612251 -1.7485462 ]
[ 1.07188379 -0.20772515]
[ 0.38738955 -0.59130272]
[ 0.74403715 0.77043827]
[-0.48569562 -1.846244 ]
[ 0.92480346 0.03211848]
[ 0.01138804 -1.03056578]
[-0.10982834 -2.64521111]
[ 0.43922201 -0.06308385]
[ 0.56023148 -1.75883213]
[ 0.71715934 -0.18560282]
[-0.03324333 -0.43753742]
[ 0.87248429 0.50736424]
[ 0.34908221 -0.19565627]
[ 0.1582798 -0.78945101]
[ 1.22100316 -1.61682728]
[ 0.16436725 -1.29825994]
[ 0.73521959 0.39524745]
[ 0.47469691 -0.41592689]
[ 1.23005729 -0.93020944]
[ 0.63074514 -0.41499744]
[ 0.70031506 -0.06320009]
[ 0.87135454 0.24995602]
[ 1.25231375 -0.07699807]
[ 1.35386953 0.33020546]
[ 0.66258066 -0.2251735 ]
[-0.04012419 -1.05518358]
[ 0.13035846 -1.55705555]
[ 0.02337438 -1.56722524]
[ 0.2407318 -0.7746612 ]
[ 1.05755171 -0.6317269 ]
[ 0.22323093 -0.28681266]
[ 0.42770626 0.84275892]
[ 1.04522645 0.52030871]
[ 1.04104379 -1.37837105]
[ 0.06935597 -0.21877043]
[ 0.28253073 -1.32488615]
[ 0.27814596 -1.11628885]
[ 0.62248441 0.02483981]
[ 0.33540673 -0.98510383]
[-0.36097409 -2.01249582]
[ 0.28762268 -0.85287312]
[ 0.09105561 -0.18058714]
[ 0.22695654 -0.38363487]
[ 0.57446378 -0.15435649]
[-0.4461723 -1.53863746]
[ 0.25587339 -0.59685229]
[ 1.83841002 0.86751506]
[ 1.15401555 -0.6965364 ]
[ 2.19790361 0.56013398]
[ 1.43534213 -0.0468307 ]
[ 1.86157577 0.2940597 ]
[ 2.74268509 0.79773671]
[ 0.36579225 -1.55628918]
[ 2.29475181 0.41866302]
[ 1.99998633 -0.70906323]
[ 2.25223216 1.9145963 ]
[ 1.35962064 0.6904434 ]
[ 1.59732747 -0.42029243]
[ 1.87761053 0.41784981]
[ 1.25590769 -1.15837974]
[ 1.46274487 -0.44079488]
[ 1.5847682 0.67398689]
[ 1.46651849 0.25476833]
[ 2.4182277 2.5481248 ]
[ 3.29964148 0.01772158]
[ 1.25954707 -1.70104672]
[ 2.03091256 0.90742744]
[ 0.97471535 -0.56985526]
[ 2.8879765 0.41225995]
[ 1.32878064 -0.4802025 ]
[ 1.6950553 1.01053648]
[ 1.94780139 1.00441272]
[ 1.17118007 -0.31533806]
[ 1.01754169 0.06413118]
[ 1.78237879 -0.18673563]
[ 1.85742501 0.56041329]
[ 2.4278203 0.25841871]
[ 2.29723178 2.61755442]
[ 1.85648383 -0.17795333]
[ 1.1104277 -0.29194458]
[ 1.19845835 -0.80860636]
[ 2.78942561 0.85394254]
[ 1.57099294 1.06501321]
[ 1.34179696 0.42102015]
[ 0.92173701 0.01716559]
[ 1.84586124 0.67387065]
[ 2.00808316 0.61183593]
[ 1.89543421 0.68727307]
[ 1.15401555 -0.6965364 ]
[ 2.03374499 0.86462403]
[ 1.99147547 1.04566567]
[ 1.86425786 0.38567404]
[ 1.55935649 -0.89369285]
[ 1.51609145 0.26817075]
[ 1.36820418 1.00787793]
[ 0.95744849 -0.02425043]]
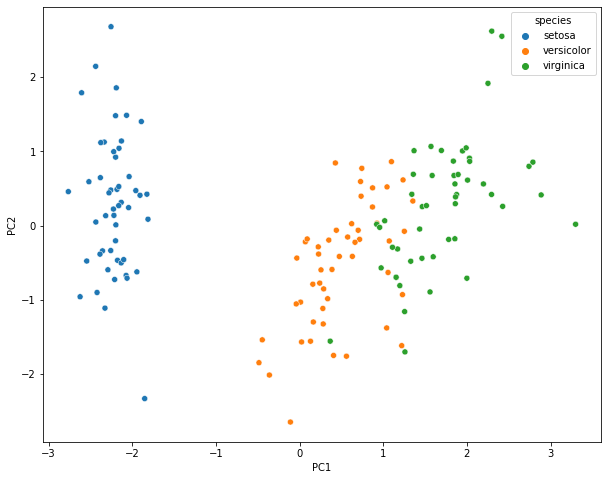
iris_transform_df = pd.DataFrame(PCs, columns=("PC1", "PC2"))
iris_transform_df = pd.concat([iris_transform_df, y], axis = 1)
iris_transform_df.head()
fig, ax = plt.subplots(figsize = (10,8))
ax_0 = sns.scatterplot("PC1", "PC2", data= iris_transform_df, hue= "species")
plt.show()
/usr/local/lib/python3.7/dist-packages/seaborn/_decorators.py:43: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.
FutureWarning
# The art of enabling machine to form rules and find trends from data without explicitly programming them is known as Machine Learning
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import numpy as np
dataset = pd.read_csv("/content/drive/MyDrive/Diabetes/diabetes.txt", delimiter= "\t")
dataset.head()
| AGE | SEX | BMI | BP | S1 | S2 | S3 | S4 | S5 | S6 | Y | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 59 | 2 | 32.1 | 101.0 | 157 | 93.2 | 38.0 | 4.0 | 4.8598 | 87 | 151 |
| 1 | 48 | 1 | 21.6 | 87.0 | 183 | 103.2 | 70.0 | 3.0 | 3.8918 | 69 | 75 |
| 2 | 72 | 2 | 30.5 | 93.0 | 156 | 93.6 | 41.0 | 4.0 | 4.6728 | 85 | 141 |
| 3 | 24 | 1 | 25.3 | 84.0 | 198 | 131.4 | 40.0 | 5.0 | 4.8903 | 89 | 206 |
| 4 | 50 | 1 | 23.0 | 101.0 | 192 | 125.4 | 52.0 | 4.0 | 4.2905 | 80 | 135 |
print(dataset.info())
print("----------------------------------------------------------------------")
print(dataset.isna().sum())
print("---------------------------------------------------------------------")
print(dataset.describe().T)
# Seperate the dataset into independent and depent features
X = dataset.iloc[:, :-1]
print(X)
print("-------------------------------------------------------------------------")
y= dataset.iloc[:, -1]
print(y)
AGE SEX BMI BP S1 S2 S3 S4 S5 S6
0 59 2 32.1 101.00 157 93.2 38.0 4.00 4.8598 87
1 48 1 21.6 87.00 183 103.2 70.0 3.00 3.8918 69
2 72 2 30.5 93.00 156 93.6 41.0 4.00 4.6728 85
3 24 1 25.3 84.00 198 131.4 40.0 5.00 4.8903 89
4 50 1 23.0 101.00 192 125.4 52.0 4.00 4.2905 80
.. ... ... ... ... ... ... ... ... ... ...
437 60 2 28.2 112.00 185 113.8 42.0 4.00 4.9836 93
438 47 2 24.9 75.00 225 166.0 42.0 5.00 4.4427 102
439 60 2 24.9 99.67 162 106.6 43.0 3.77 4.1271 95
440 36 1 30.0 95.00 201 125.2 42.0 4.79 5.1299 85
441 36 1 19.6 71.00 250 133.2 97.0 3.00 4.5951 92
[442 rows x 10 columns]
-------------------------------------------------------------------------
0 151
1 75
2 141
3 206
4 135
...
437 178
438 104
439 132
440 220
441 57
Name: Y, Length: 442, dtype: int64
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= 0.2, random_state = 110)
print(X_train)
print(X_test)
print("-----------------------------------------------------")
print(y_train)
print(y_test)
AGE SEX BMI BP S1 S2 S3 S4 S5 S6
96 64 2 27.3 109.00 186 107.6 38.0 5.00 5.3083 99
333 56 2 25.8 103.00 177 114.4 34.0 5.00 4.9628 99
317 54 1 23.2 110.67 238 162.8 48.0 4.96 4.9127 108
239 55 1 28.2 91.00 250 140.2 67.0 4.00 5.3660 103
113 54 2 27.7 113.00 200 128.4 37.0 5.00 5.1533 113
.. ... ... ... ... ... ... ... ... ... ...
381 29 2 18.1 73.00 158 99.0 41.0 4.00 4.4998 78
271 59 2 27.2 107.00 158 102.0 39.0 4.00 4.4427 93
61 37 2 26.8 79.00 157 98.0 28.0 6.00 5.0434 96
227 67 2 23.6 111.33 189 105.4 70.0 2.70 4.2195 93
128 34 1 20.6 87.00 185 112.2 58.0 3.00 4.3041 74
[353 rows x 10 columns]
AGE SEX BMI BP S1 S2 S3 S4 S5 S6
294 55 2 23.5 93.00 177 126.8 41.0 4.00 3.8286 83
159 47 1 30.4 120.00 199 120.0 46.0 4.00 5.1059 87
312 28 1 24.2 93.00 174 106.4 54.0 3.00 4.2195 84
119 53 1 22.0 94.00 175 88.0 59.0 3.00 4.9416 98
134 28 1 30.4 85.00 198 115.6 67.0 3.00 4.3438 80
.. ... ... ... ... ... ... ... ... ... ...
414 71 2 27.0 93.33 269 190.2 41.0 6.56 5.2417 93
166 33 2 20.8 84.00 125 70.2 46.0 3.00 3.7842 66
434 53 1 26.5 97.00 193 122.4 58.0 3.00 4.1431 99
390 51 2 32.8 112.00 202 100.6 37.0 5.00 5.7746 109
168 49 2 31.9 94.00 234 155.8 34.0 7.00 5.3982 122
[89 rows x 10 columns]
-----------------------------------------------------
96 150
333 164
317 190
239 262
113 297
...
381 104
271 127
61 144
227 108
128 115
Name: Y, Length: 353, dtype: int64
294 55
159 195
312 144
119 200
134 103
...
414 131
166 70
434 49
390 277
168 268
Name: Y, Length: 89, dtype: int64
from sklearn.linear_model import LinearRegression
L_regressor = LinearRegression()
L_regressor.fit(X_train, y_train)
#---- test model on test data X_test
prediction = L_regressor.predict(X_test)
print(prediction)
print(y_test)
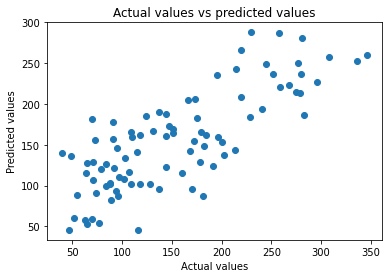
plt.scatter(y_test, prediction)
plt.xlabel("Actual values")
plt.ylabel("Predicted values")
plt.title("Actual values vs predicted values")
[ 88.7257154 236.01349565 122.82671275 152.91194894 133.26299572
155.10995617 108.45070799 166.16370245 206.40303033 227.12512886
45.58436461 257.33397866 188.25079196 143.91214004 101.58303786
129.18862987 157.18468301 140.00779148 142.28184775 115.48953396
129.15211612 182.9636348 52.25034904 286.86546595 242.7761079
46.07643676 146.37057691 125.90228716 137.64669731 102.12906943
159.294184 127.19797503 120.2095064 189.73221207 121.94777703
87.58871142 162.09127654 214.57935651 100.0105965 265.88447661
237.09032754 102.23950004 115.64512814 193.83264705 185.47519786
186.85928531 281.30774621 86.98229992 220.56270381 141.45606787
101.56547169 173.03077936 96.25903702 159.50774879 53.63613547
208.84468478 165.93698745 124.42552414 160.59146202 248.64622776
103.47508113 148.42042807 205.43430394 93.90192239 161.46649216
91.00134606 253.13344701 96.16425468 164.29821281 181.27263938
58.24275384 116.28152401 183.49639474 169.54560591 110.11920824
236.24602514 59.7852014 155.27187615 287.9524243 213.84063469
82.59836521 259.69744698 178.24353173 107.16945725 167.34950979
58.7571307 135.75101228 250.65478989 223.09415657]
294 55
159 195
312 144
119 200
134 103
...
414 131
166 70
434 49
390 277
168 268
Name: Y, Length: 89, dtype: int64
Text(0.5, 1.0, 'Actual values vs predicted values')
from sklearn import metrics
print("Mean absolute error : ", metrics.mean_absolute_percentage_error(y_test, prediction))
print("Mean squared error :", metrics.mean_squared_error(y_test, prediction))
Mean absolute error : 0.3300922548696817
Mean squared error : 2228.090831059464
# Intercept and coefcient parameters
print(L_regressor.intercept_)
print("------------------------")
print(L_regressor.coef_)
# Map coeffients with features
coef_df = pd.DataFrame(L_regressor.coef_, X.columns, columns= ["Coeffcient"])
coef_df
-307.57104546505354
------------------------
[ 1.40608997e-01 -2.56128390e+01 5.08771783e+00 1.19293496e+00
-1.08819176e+00 8.03227722e-01 4.24108443e-02 4.53744471e+00
6.51304992e+01 3.71060693e-01]
| Coeffcient | |
|---|---|
| AGE | 0.140609 |
| SEX | -25.612839 |
| BMI | 5.087718 |
| BP | 1.192935 |
| S1 | -1.088192 |
| S2 | 0.803228 |
| S3 | 0.042411 |
| S4 | 4.537445 |
| S5 | 65.130499 |
| S6 | 0.371061 |
Logistic Regression#
import pandas as pd
dataset = pd.read_csv("/content/drive/MyDrive/Breast Cancer Data/Breast_cancer_data.csv")
print(dataset.head())
print("------------------------------------------------------------------------------")
print(dataset.columns)
id diagnosis radius_mean texture_mean perimeter_mean area_mean \
0 842302 M 17.99 10.38 122.80 1001.0
1 842517 M 20.57 17.77 132.90 1326.0
2 84300903 M 19.69 21.25 130.00 1203.0
3 84348301 M 11.42 20.38 77.58 386.1
4 84358402 M 20.29 14.34 135.10 1297.0
smoothness_mean compactness_mean concavity_mean concave points_mean \
0 0.11840 0.27760 0.3001 0.14710
1 0.08474 0.07864 0.0869 0.07017
2 0.10960 0.15990 0.1974 0.12790
3 0.14250 0.28390 0.2414 0.10520
4 0.10030 0.13280 0.1980 0.10430
... texture_worst perimeter_worst area_worst smoothness_worst \
0 ... 17.33 184.60 2019.0 0.1622
1 ... 23.41 158.80 1956.0 0.1238
2 ... 25.53 152.50 1709.0 0.1444
3 ... 26.50 98.87 567.7 0.2098
4 ... 16.67 152.20 1575.0 0.1374
compactness_worst concavity_worst concave points_worst symmetry_worst \
0 0.6656 0.7119 0.2654 0.4601
1 0.1866 0.2416 0.1860 0.2750
2 0.4245 0.4504 0.2430 0.3613
3 0.8663 0.6869 0.2575 0.6638
4 0.2050 0.4000 0.1625 0.2364
fractal_dimension_worst Unnamed: 32
0 0.11890 NaN
1 0.08902 NaN
2 0.08758 NaN
3 0.17300 NaN
4 0.07678 NaN
[5 rows x 33 columns]
------------------------------------------------------------------------------
Index(['id', 'diagnosis', 'radius_mean', 'texture_mean', 'perimeter_mean',
'area_mean', 'smoothness_mean', 'compactness_mean', 'concavity_mean',
'concave points_mean', 'symmetry_mean', 'fractal_dimension_mean',
'radius_se', 'texture_se', 'perimeter_se', 'area_se', 'smoothness_se',
'compactness_se', 'concavity_se', 'concave points_se', 'symmetry_se',
'fractal_dimension_se', 'radius_worst', 'texture_worst',
'perimeter_worst', 'area_worst', 'smoothness_worst',
'compactness_worst', 'concavity_worst', 'concave points_worst',
'symmetry_worst', 'fractal_dimension_worst', 'Unnamed: 32'],
dtype='object')
dataset.T.head()
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ... | 559 | 560 | 561 | 562 | 563 | 564 | 565 | 566 | 567 | 568 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| id | 842302 | 842517 | 84300903 | 84348301 | 84358402 | 843786 | 844359 | 84458202 | 844981 | 84501001 | ... | 925291 | 925292 | 925311 | 925622 | 926125 | 926424 | 926682 | 926954 | 927241 | 92751 |
| diagnosis | M | M | M | M | M | M | M | M | M | M | ... | B | B | B | M | M | M | M | M | M | B |
| radius_mean | 17.99 | 20.57 | 19.69 | 11.42 | 20.29 | 12.45 | 18.25 | 13.71 | 13.0 | 12.46 | ... | 11.51 | 14.05 | 11.2 | 15.22 | 20.92 | 21.56 | 20.13 | 16.6 | 20.6 | 7.76 |
| texture_mean | 10.38 | 17.77 | 21.25 | 20.38 | 14.34 | 15.7 | 19.98 | 20.83 | 21.82 | 24.04 | ... | 23.93 | 27.15 | 29.37 | 30.62 | 25.09 | 22.39 | 28.25 | 28.08 | 29.33 | 24.54 |
| perimeter_mean | 122.8 | 132.9 | 130.0 | 77.58 | 135.1 | 82.57 | 119.6 | 90.2 | 87.5 | 83.97 | ... | 74.52 | 91.38 | 70.67 | 103.4 | 143.0 | 142.0 | 131.2 | 108.3 | 140.1 | 47.92 |
5 rows × 569 columns
# we can see dataset columns id and Unnamed:32 are not required , so we can drop those columns
dataset = dataset.drop(["id", "Unnamed: 32"], axis=1)
print(dataset.head())
---------------------------------------------------------------------------
KeyError Traceback (most recent call last)
<ipython-input-20-926d8a94ccd3> in <module>()
1 # we can see dataset columns id and Unnamed:32 are not required , so we can drop those columns
----> 2 dataset = dataset.drop(["id", "Unnamed: 32"], axis=1)
3 print(dataset.head())
/usr/local/lib/python3.7/dist-packages/pandas/util/_decorators.py in wrapper(*args, **kwargs)
309 stacklevel=stacklevel,
310 )
--> 311 return func(*args, **kwargs)
312
313 return wrapper
/usr/local/lib/python3.7/dist-packages/pandas/core/frame.py in drop(self, labels, axis, index, columns, level, inplace, errors)
4911 level=level,
4912 inplace=inplace,
-> 4913 errors=errors,
4914 )
4915
/usr/local/lib/python3.7/dist-packages/pandas/core/generic.py in drop(self, labels, axis, index, columns, level, inplace, errors)
4148 for axis, labels in axes.items():
4149 if labels is not None:
-> 4150 obj = obj._drop_axis(labels, axis, level=level, errors=errors)
4151
4152 if inplace:
/usr/local/lib/python3.7/dist-packages/pandas/core/generic.py in _drop_axis(self, labels, axis, level, errors)
4183 new_axis = axis.drop(labels, level=level, errors=errors)
4184 else:
-> 4185 new_axis = axis.drop(labels, errors=errors)
4186 result = self.reindex(**{axis_name: new_axis})
4187
/usr/local/lib/python3.7/dist-packages/pandas/core/indexes/base.py in drop(self, labels, errors)
6015 if mask.any():
6016 if errors != "ignore":
-> 6017 raise KeyError(f"{labels[mask]} not found in axis")
6018 indexer = indexer[~mask]
6019 return self.delete(indexer)
KeyError: "['id' 'Unnamed: 32'] not found in axis"
print(dataset.describe().T)
print("----------------------------------------------------------------------------------------------")
print(dataset.info())
count mean std min \
radius_mean 569.0 14.127292 3.524049 6.981000
texture_mean 569.0 19.289649 4.301036 9.710000
perimeter_mean 569.0 91.969033 24.298981 43.790000
area_mean 569.0 654.889104 351.914129 143.500000
smoothness_mean 569.0 0.096360 0.014064 0.052630
compactness_mean 569.0 0.104341 0.052813 0.019380
concavity_mean 569.0 0.088799 0.079720 0.000000
concave points_mean 569.0 0.048919 0.038803 0.000000
symmetry_mean 569.0 0.181162 0.027414 0.106000
fractal_dimension_mean 569.0 0.062798 0.007060 0.049960
radius_se 569.0 0.405172 0.277313 0.111500
texture_se 569.0 1.216853 0.551648 0.360200
perimeter_se 569.0 2.866059 2.021855 0.757000
area_se 569.0 40.337079 45.491006 6.802000
smoothness_se 569.0 0.007041 0.003003 0.001713
compactness_se 569.0 0.025478 0.017908 0.002252
concavity_se 569.0 0.031894 0.030186 0.000000
concave points_se 569.0 0.011796 0.006170 0.000000
symmetry_se 569.0 0.020542 0.008266 0.007882
fractal_dimension_se 569.0 0.003795 0.002646 0.000895
radius_worst 569.0 16.269190 4.833242 7.930000
texture_worst 569.0 25.677223 6.146258 12.020000
perimeter_worst 569.0 107.261213 33.602542 50.410000
area_worst 569.0 880.583128 569.356993 185.200000
smoothness_worst 569.0 0.132369 0.022832 0.071170
compactness_worst 569.0 0.254265 0.157336 0.027290
concavity_worst 569.0 0.272188 0.208624 0.000000
concave points_worst 569.0 0.114606 0.065732 0.000000
symmetry_worst 569.0 0.290076 0.061867 0.156500
fractal_dimension_worst 569.0 0.083946 0.018061 0.055040
25% 50% 75% max
radius_mean 11.700000 13.370000 15.780000 28.11000
texture_mean 16.170000 18.840000 21.800000 39.28000
perimeter_mean 75.170000 86.240000 104.100000 188.50000
area_mean 420.300000 551.100000 782.700000 2501.00000
smoothness_mean 0.086370 0.095870 0.105300 0.16340
compactness_mean 0.064920 0.092630 0.130400 0.34540
concavity_mean 0.029560 0.061540 0.130700 0.42680
concave points_mean 0.020310 0.033500 0.074000 0.20120
symmetry_mean 0.161900 0.179200 0.195700 0.30400
fractal_dimension_mean 0.057700 0.061540 0.066120 0.09744
radius_se 0.232400 0.324200 0.478900 2.87300
texture_se 0.833900 1.108000 1.474000 4.88500
perimeter_se 1.606000 2.287000 3.357000 21.98000
area_se 17.850000 24.530000 45.190000 542.20000
smoothness_se 0.005169 0.006380 0.008146 0.03113
compactness_se 0.013080 0.020450 0.032450 0.13540
concavity_se 0.015090 0.025890 0.042050 0.39600
concave points_se 0.007638 0.010930 0.014710 0.05279
symmetry_se 0.015160 0.018730 0.023480 0.07895
fractal_dimension_se 0.002248 0.003187 0.004558 0.02984
radius_worst 13.010000 14.970000 18.790000 36.04000
texture_worst 21.080000 25.410000 29.720000 49.54000
perimeter_worst 84.110000 97.660000 125.400000 251.20000
area_worst 515.300000 686.500000 1084.000000 4254.00000
smoothness_worst 0.116600 0.131300 0.146000 0.22260
compactness_worst 0.147200 0.211900 0.339100 1.05800
concavity_worst 0.114500 0.226700 0.382900 1.25200
concave points_worst 0.064930 0.099930 0.161400 0.29100
symmetry_worst 0.250400 0.282200 0.317900 0.66380
fractal_dimension_worst 0.071460 0.080040 0.092080 0.20750
----------------------------------------------------------------------------------------------
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 569 entries, 0 to 568
Data columns (total 31 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 diagnosis 569 non-null object
1 radius_mean 569 non-null float64
2 texture_mean 569 non-null float64
3 perimeter_mean 569 non-null float64
4 area_mean 569 non-null float64
5 smoothness_mean 569 non-null float64
6 compactness_mean 569 non-null float64
7 concavity_mean 569 non-null float64
8 concave points_mean 569 non-null float64
9 symmetry_mean 569 non-null float64
10 fractal_dimension_mean 569 non-null float64
11 radius_se 569 non-null float64
12 texture_se 569 non-null float64
13 perimeter_se 569 non-null float64
14 area_se 569 non-null float64
15 smoothness_se 569 non-null float64
16 compactness_se 569 non-null float64
17 concavity_se 569 non-null float64
18 concave points_se 569 non-null float64
19 symmetry_se 569 non-null float64
20 fractal_dimension_se 569 non-null float64
21 radius_worst 569 non-null float64
22 texture_worst 569 non-null float64
23 perimeter_worst 569 non-null float64
24 area_worst 569 non-null float64
25 smoothness_worst 569 non-null float64
26 compactness_worst 569 non-null float64
27 concavity_worst 569 non-null float64
28 concave points_worst 569 non-null float64
29 symmetry_worst 569 non-null float64
30 fractal_dimension_worst 569 non-null float64
dtypes: float64(30), object(1)
memory usage: 137.9+ KB
None
print(dataset.diagnosis.value_counts())
print(dataset.iloc[:,0])
print(dataset.head(2))
B 357
M 212
Name: diagnosis, dtype: int64
0 M
1 M
2 M
3 M
4 M
..
564 M
565 M
566 M
567 M
568 B
Name: diagnosis, Length: 569, dtype: object
diagnosis radius_mean texture_mean perimeter_mean area_mean \
0 M 17.99 10.38 122.8 1001.0
1 M 20.57 17.77 132.9 1326.0
smoothness_mean compactness_mean concavity_mean concave points_mean \
0 0.11840 0.27760 0.3001 0.14710
1 0.08474 0.07864 0.0869 0.07017
symmetry_mean ... radius_worst texture_worst perimeter_worst \
0 0.2419 ... 25.38 17.33 184.6
1 0.1812 ... 24.99 23.41 158.8
area_worst smoothness_worst compactness_worst concavity_worst \
0 2019.0 0.1622 0.6656 0.7119
1 1956.0 0.1238 0.1866 0.2416
concave points_worst symmetry_worst fractal_dimension_worst
0 0.2654 0.4601 0.11890
1 0.1860 0.2750 0.08902
[2 rows x 31 columns]
X = dataset.iloc[:, 1:]
print(X)
y= dataset.iloc[:, 0]
print(y)
radius_mean texture_mean perimeter_mean area_mean smoothness_mean \
0 17.99 10.38 122.80 1001.0 0.11840
1 20.57 17.77 132.90 1326.0 0.08474
2 19.69 21.25 130.00 1203.0 0.10960
3 11.42 20.38 77.58 386.1 0.14250
4 20.29 14.34 135.10 1297.0 0.10030
.. ... ... ... ... ...
564 21.56 22.39 142.00 1479.0 0.11100
565 20.13 28.25 131.20 1261.0 0.09780
566 16.60 28.08 108.30 858.1 0.08455
567 20.60 29.33 140.10 1265.0 0.11780
568 7.76 24.54 47.92 181.0 0.05263
compactness_mean concavity_mean concave points_mean symmetry_mean \
0 0.27760 0.30010 0.14710 0.2419
1 0.07864 0.08690 0.07017 0.1812
2 0.15990 0.19740 0.12790 0.2069
3 0.28390 0.24140 0.10520 0.2597
4 0.13280 0.19800 0.10430 0.1809
.. ... ... ... ...
564 0.11590 0.24390 0.13890 0.1726
565 0.10340 0.14400 0.09791 0.1752
566 0.10230 0.09251 0.05302 0.1590
567 0.27700 0.35140 0.15200 0.2397
568 0.04362 0.00000 0.00000 0.1587
fractal_dimension_mean ... radius_worst texture_worst \
0 0.07871 ... 25.380 17.33
1 0.05667 ... 24.990 23.41
2 0.05999 ... 23.570 25.53
3 0.09744 ... 14.910 26.50
4 0.05883 ... 22.540 16.67
.. ... ... ... ...
564 0.05623 ... 25.450 26.40
565 0.05533 ... 23.690 38.25
566 0.05648 ... 18.980 34.12
567 0.07016 ... 25.740 39.42
568 0.05884 ... 9.456 30.37
perimeter_worst area_worst smoothness_worst compactness_worst \
0 184.60 2019.0 0.16220 0.66560
1 158.80 1956.0 0.12380 0.18660
2 152.50 1709.0 0.14440 0.42450
3 98.87 567.7 0.20980 0.86630
4 152.20 1575.0 0.13740 0.20500
.. ... ... ... ...
564 166.10 2027.0 0.14100 0.21130
565 155.00 1731.0 0.11660 0.19220
566 126.70 1124.0 0.11390 0.30940
567 184.60 1821.0 0.16500 0.86810
568 59.16 268.6 0.08996 0.06444
concavity_worst concave points_worst symmetry_worst \
0 0.7119 0.2654 0.4601
1 0.2416 0.1860 0.2750
2 0.4504 0.2430 0.3613
3 0.6869 0.2575 0.6638
4 0.4000 0.1625 0.2364
.. ... ... ...
564 0.4107 0.2216 0.2060
565 0.3215 0.1628 0.2572
566 0.3403 0.1418 0.2218
567 0.9387 0.2650 0.4087
568 0.0000 0.0000 0.2871
fractal_dimension_worst
0 0.11890
1 0.08902
2 0.08758
3 0.17300
4 0.07678
.. ...
564 0.07115
565 0.06637
566 0.07820
567 0.12400
568 0.07039
[569 rows x 30 columns]
0 M
1 M
2 M
3 M
4 M
..
564 M
565 M
566 M
567 M
568 B
Name: diagnosis, Length: 569, dtype: object
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_norm = sc.fit_transform(X)
print(X_norm)
[[ 1.09706398 -2.07333501 1.26993369 ... 2.29607613 2.75062224
1.93701461]
[ 1.82982061 -0.35363241 1.68595471 ... 1.0870843 -0.24388967
0.28118999]
[ 1.57988811 0.45618695 1.56650313 ... 1.95500035 1.152255
0.20139121]
...
[ 0.70228425 2.0455738 0.67267578 ... 0.41406869 -1.10454895
-0.31840916]
[ 1.83834103 2.33645719 1.98252415 ... 2.28998549 1.91908301
2.21963528]
[-1.80840125 1.22179204 -1.81438851 ... -1.74506282 -0.04813821
-0.75120669]]
# split normalized data
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_norm,y, test_size= 0.2, random_state = 101)
# initialize the classifier
from sklearn.linear_model import LogisticRegression
Log_classifier = LogisticRegression(random_state=0)
Log_classifier.fit(X_train, y_train)
#----
y_pred = Log_classifier.predict(X_test)
print(y_pred)
# compare y_pred vs actual y_test
print("-----------------------------------------------------------------")
print(y_test)
['B' 'B' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'B'
'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'B' 'M' 'M' 'B' 'M' 'B' 'M' 'B' 'B'
'M' 'M' 'M' 'M' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'B' 'M' 'B' 'B' 'M'
'B' 'B' 'M' 'M' 'B' 'B' 'M' 'M' 'B' 'B' 'M' 'B' 'B' 'M' 'M' 'B' 'M' 'B'
'B' 'B' 'M' 'M' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'M'
'B' 'M' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'M']
-----------------------------------------------------------------
107 B
437 B
195 B
141 M
319 B
..
19 B
313 B
139 B
495 B
317 M
Name: diagnosis, Length: 114, dtype: object
# Model evaluation
from sklearn.metrics import confusion_matrix, classification_report
cm = confusion_matrix( y_test, y_pred)
print(cm)
print("---------------------------------------------------------------------------")
print("classification report \n", classification_report(y_test, y_pred))
[[72 0]
[ 1 41]]
---------------------------------------------------------------------------
classification report
precision recall f1-score support
B 0.99 1.00 0.99 72
M 1.00 0.98 0.99 42
accuracy 0.99 114
macro avg 0.99 0.99 0.99 114
weighted avg 0.99 0.99 0.99 114
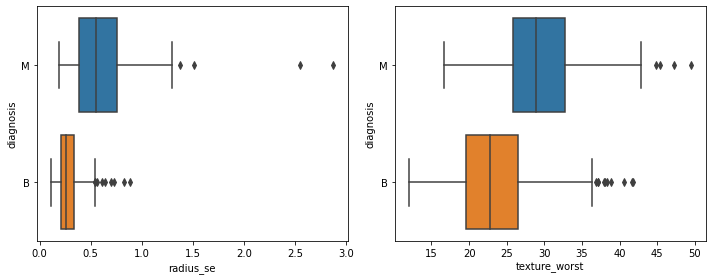
# --- Getting informative features by getting coeffcients
coeff_df = pd.DataFrame(Log_classifier.coef_.T, X.columns,
columns=['Coefficient'])
coeff_df =coeff_df.sort_values(by=['Coefficient'],ascending=False)
coeff_df
# the features “radius_se” and “texture_worst” have a major contribution to determining the malignancy
| Coefficient | |
|---|---|
| radius_se | 1.379673 |
| texture_worst | 1.169080 |
| concave points_mean | 1.156939 |
| area_se | 0.984579 |
| concave points_worst | 0.933089 |
| radius_worst | 0.903471 |
| smoothness_worst | 0.872462 |
| area_worst | 0.846826 |
| concavity_mean | 0.807876 |
| concavity_worst | 0.802358 |
| perimeter_se | 0.637758 |
| fractal_dimension_worst | 0.618413 |
| perimeter_worst | 0.568124 |
| symmetry_worst | 0.562905 |
| texture_mean | 0.387553 |
| area_mean | 0.314432 |
| concave points_se | 0.267092 |
| radius_mean | 0.266278 |
| perimeter_mean | 0.232904 |
| compactness_worst | 0.052849 |
| symmetry_mean | 0.042495 |
| smoothness_mean | -0.036783 |
| symmetry_se | -0.042753 |
| smoothness_se | -0.135624 |
| texture_se | -0.153152 |
| concavity_se | -0.224247 |
| fractal_dimension_mean | -0.378132 |
| compactness_mean | -0.590002 |
| fractal_dimension_se | -0.697663 |
| compactness_se | -0.780794 |
fig, axes = plt.subplots(nrows=1, ncols=2,figsize=(10,4))
sns.boxplot(x="radius_se", y="diagnosis", data=dataset,ax=axes[0])
sns.boxplot(x='texture_worst',y='diagnosis',
data=dataset,ax=axes[1])
fig.tight_layout()
Decision Trees and Random Forest#
# Decision tree is based on whole dataset,
# Where as Random FOrest incidently selects features to create different decsion trees
#--- Tree Pruning --- constructing too many decision trees leads to overfitting , so for real world data we have to restrict decison tree by keeping little impurities tolerable is called tree pruining
# Random forest trains multiple decision trees on sample data set and samples are selected randomly with replacements (Bootstrap sampling)
# Random forest model ~= Ensemble Methods
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
dataset = pd.read_csv("/content/drive/MyDrive/Breast Cancer Data/Breast_cancer_data.csv")
print(dataset.head())
print("------------------------------------------------------------------------------")
print(dataset.columns)
id diagnosis radius_mean texture_mean perimeter_mean area_mean \
0 842302 M 17.99 10.38 122.80 1001.0
1 842517 M 20.57 17.77 132.90 1326.0
2 84300903 M 19.69 21.25 130.00 1203.0
3 84348301 M 11.42 20.38 77.58 386.1
4 84358402 M 20.29 14.34 135.10 1297.0
smoothness_mean compactness_mean concavity_mean concave points_mean \
0 0.11840 0.27760 0.3001 0.14710
1 0.08474 0.07864 0.0869 0.07017
2 0.10960 0.15990 0.1974 0.12790
3 0.14250 0.28390 0.2414 0.10520
4 0.10030 0.13280 0.1980 0.10430
... texture_worst perimeter_worst area_worst smoothness_worst \
0 ... 17.33 184.60 2019.0 0.1622
1 ... 23.41 158.80 1956.0 0.1238
2 ... 25.53 152.50 1709.0 0.1444
3 ... 26.50 98.87 567.7 0.2098
4 ... 16.67 152.20 1575.0 0.1374
compactness_worst concavity_worst concave points_worst symmetry_worst \
0 0.6656 0.7119 0.2654 0.4601
1 0.1866 0.2416 0.1860 0.2750
2 0.4245 0.4504 0.2430 0.3613
3 0.8663 0.6869 0.2575 0.6638
4 0.2050 0.4000 0.1625 0.2364
fractal_dimension_worst Unnamed: 32
0 0.11890 NaN
1 0.08902 NaN
2 0.08758 NaN
3 0.17300 NaN
4 0.07678 NaN
[5 rows x 33 columns]
------------------------------------------------------------------------------
Index(['id', 'diagnosis', 'radius_mean', 'texture_mean', 'perimeter_mean',
'area_mean', 'smoothness_mean', 'compactness_mean', 'concavity_mean',
'concave points_mean', 'symmetry_mean', 'fractal_dimension_mean',
'radius_se', 'texture_se', 'perimeter_se', 'area_se', 'smoothness_se',
'compactness_se', 'concavity_se', 'concave points_se', 'symmetry_se',
'fractal_dimension_se', 'radius_worst', 'texture_worst',
'perimeter_worst', 'area_worst', 'smoothness_worst',
'compactness_worst', 'concavity_worst', 'concave points_worst',
'symmetry_worst', 'fractal_dimension_worst', 'Unnamed: 32'],
dtype='object')
# dataset = dataset.drop(["id", 'Unnamed: 32'], axis=1)
dataset.columns
Index(['diagnosis', 'radius_mean', 'texture_mean', 'perimeter_mean',
'area_mean', 'smoothness_mean', 'compactness_mean', 'concavity_mean',
'concave points_mean', 'symmetry_mean', 'fractal_dimension_mean',
'radius_se', 'texture_se', 'perimeter_se', 'area_se', 'smoothness_se',
'compactness_se', 'concavity_se', 'concave points_se', 'symmetry_se',
'fractal_dimension_se', 'radius_worst', 'texture_worst',
'perimeter_worst', 'area_worst', 'smoothness_worst',
'compactness_worst', 'concavity_worst', 'concave points_worst',
'symmetry_worst', 'fractal_dimension_worst'],
dtype='object')
#--- Train test split
X = dataset.iloc[:, 1:]
y = dataset.iloc[:, 0]
print(X)
print(":=========================:")
print(y)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
print(X_train, X_test)
# Decision tree call and train on data
from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier()
classifier.fit(X_train, y_train)
DecisionTreeClassifier()
# prediction and evaluation
preds = classifier.predict(X_test)
# Evaluation
from sklearn.metrics import confusion_matrix, classification_report
print(classification_report(y_test, preds))
precision recall f1-score support
B 0.94 0.88 0.91 105
M 0.82 0.91 0.86 66
accuracy 0.89 171
macro avg 0.88 0.89 0.88 171
weighted avg 0.89 0.89 0.89 171
# random forest from ensemble methods
from sklearn.ensemble import RandomForestClassifier
rfc_classifier = RandomForestClassifier(n_estimators= 300)
rfc_classifier.fit(X_train, y_train)
rfc_pred = rfc_classifier.predict(X_test)
print(classification_report(y_test, rfc_pred))
precision recall f1-score support
B 0.99 0.96 0.98 105
M 0.94 0.98 0.96 66
accuracy 0.97 171
macro avg 0.97 0.97 0.97 171
weighted avg 0.97 0.97 0.97 171
#Cross validation and prediction
from sklearn.model_selection import cross_validate
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators=100)
cross_validator = cross_validate(classifier, X, y, cv=5,scoring = 'accuracy',return_estimator = 'true')
print(cross_validator['test_score'])
[0.93859649 0.94736842 0.99122807 0.97368421 0.98230088]
# so highest value from above is best model .
# here best model is 0.00122807
best_model = cross_validator["estimator"][-1]
best_model
rfc_best_pred = best_model.predict(X_test)
print(classification_report(y_test, rfc_best_pred))
precision recall f1-score support
B 1.00 0.99 1.00 105
M 0.99 1.00 0.99 66
accuracy 0.99 171
macro avg 0.99 1.00 0.99 171
weighted avg 0.99 0.99 0.99 171
Support vector Machines (SVMs)#
# Support vector machines are linear classifier , they make linear decision boundaries
# SVMs goal is to find the Hyperplane or decision boundaries , which best fit and seperates n dimensional into classes .
# if suppose one dimensional data is not having linear seperable (as of real world data), then we use kernel trick to ass another feature (dimension) there by separating points or data
# Radiab basis function (RBF ) is an example
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
#--- Wheat seed Dataset
dataset = pd.read_csv("/content/drive/MyDrive/Wheat_seed_dataset/wheat_seeds.csv")
print(dataset.info())
dataset.head()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 199 entries, 0 to 198
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Area 199 non-null float64
1 Perimeter 199 non-null float64
2 Compactness 199 non-null float64
3 Kernel.Length 199 non-null float64
4 Kernel.Width 199 non-null float64
5 Asymmetry.Coeff 199 non-null float64
6 Kernel.Groove 199 non-null float64
7 Type 199 non-null int64
dtypes: float64(7), int64(1)
memory usage: 12.6 KB
None
| Area | Perimeter | Compactness | Kernel.Length | Kernel.Width | Asymmetry.Coeff | Kernel.Groove | Type | |
|---|---|---|---|---|---|---|---|---|
| 0 | 15.26 | 14.84 | 0.8710 | 5.763 | 3.312 | 2.221 | 5.220 | 1 |
| 1 | 14.88 | 14.57 | 0.8811 | 5.554 | 3.333 | 1.018 | 4.956 | 1 |
| 2 | 14.29 | 14.09 | 0.9050 | 5.291 | 3.337 | 2.699 | 4.825 | 1 |
| 3 | 13.84 | 13.94 | 0.8955 | 5.324 | 3.379 | 2.259 | 4.805 | 1 |
| 4 | 16.14 | 14.99 | 0.9034 | 5.658 | 3.562 | 1.355 | 5.175 | 1 |
dataset["Type"].value_counts()
2 68
1 66
3 65
Name: Type, dtype: int64
dataset.isnull().sum()
Area 0
Perimeter 0
Compactness 0
Kernel.Length 0
Kernel.Width 0
Asymmetry.Coeff 0
Kernel.Groove 0
Type 0
dtype: int64
# Split data Train Test split
X = dataset.iloc[:, 0:-1]
print(X)
y= dataset.iloc[:, -1]
print(y)
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 10)
print(X_train)
print(X_test)
Area Perimeter Compactness Kernel.Length Kernel.Width \
0 15.26 14.84 0.8710 5.763 3.312
1 14.88 14.57 0.8811 5.554 3.333
2 14.29 14.09 0.9050 5.291 3.337
3 13.84 13.94 0.8955 5.324 3.379
4 16.14 14.99 0.9034 5.658 3.562
.. ... ... ... ... ...
194 12.19 13.20 0.8783 5.137 2.981
195 11.23 12.88 0.8511 5.140 2.795
196 13.20 13.66 0.8883 5.236 3.232
197 11.84 13.21 0.8521 5.175 2.836
198 12.30 13.34 0.8684 5.243 2.974
Asymmetry.Coeff Kernel.Groove
0 2.221 5.220
1 1.018 4.956
2 2.699 4.825
3 2.259 4.805
4 1.355 5.175
.. ... ...
194 3.631 4.870
195 4.325 5.003
196 8.315 5.056
197 3.598 5.044
198 5.637 5.063
[199 rows x 7 columns]
0 1
1 1
2 1
3 1
4 1
..
194 3
195 3
196 3
197 3
198 3
Name: Type, Length: 199, dtype: int64
Area Perimeter Compactness Kernel.Length Kernel.Width \
24 16.19 15.16 0.8849 5.833 3.421
43 13.80 14.04 0.8794 5.376 3.155
101 18.83 16.29 0.8917 6.037 3.786
142 12.70 13.71 0.8491 5.386 2.911
21 15.88 14.90 0.8988 5.618 3.507
.. ... ... ... ... ...
113 18.89 16.23 0.9008 6.227 3.769
64 14.01 14.29 0.8625 5.609 3.158
15 13.99 13.83 0.9183 5.119 3.383
125 18.30 15.89 0.9108 5.979 3.755
9 15.26 14.85 0.8696 5.714 3.242
Asymmetry.Coeff Kernel.Groove
24 0.9030 5.307
43 1.5600 4.961
101 2.5530 5.879
142 3.2600 5.316
21 0.7651 5.091
.. ... ...
113 3.6390 5.966
64 2.2170 5.132
15 5.2340 4.781
125 2.8370 5.962
9 4.5430 5.314
[149 rows x 7 columns]
Area Perimeter Compactness Kernel.Length Kernel.Width \
59 12.36 13.19 0.8923 5.076 3.042
5 14.38 14.21 0.8951 5.386 3.312
20 14.11 14.26 0.8722 5.520 3.168
124 17.55 15.66 0.8991 5.791 3.690
52 14.52 14.60 0.8557 5.741 3.113
19 14.16 14.40 0.8584 5.658 3.129
161 12.15 13.45 0.8443 5.417 2.837
55 14.92 14.43 0.9006 5.384 3.412
69 19.11 16.26 0.9081 6.154 3.930
2 14.29 14.09 0.9050 5.291 3.337
98 19.46 16.50 0.8985 6.113 3.892
10 14.03 14.16 0.8796 5.438 3.201
75 17.12 15.55 0.8892 5.850 3.566
134 13.07 13.92 0.8480 5.472 2.994
193 12.37 13.47 0.8567 5.204 2.960
63 14.34 14.37 0.8726 5.630 3.190
110 19.06 16.45 0.8854 6.416 3.719
78 20.20 16.89 0.8894 6.285 3.864
178 10.91 12.80 0.8372 5.088 2.675
114 20.03 16.90 0.8811 6.493 3.857
149 11.19 13.05 0.8253 5.250 2.675
129 15.56 14.89 0.8823 5.776 3.408
61 12.78 13.57 0.8716 5.262 3.026
87 18.76 16.20 0.8984 6.172 3.796
102 17.63 15.86 0.8800 6.033 3.573
120 18.75 16.18 0.8999 6.111 3.869
168 10.74 12.73 0.8329 5.145 2.642
1 14.88 14.57 0.8811 5.554 3.333
47 14.86 14.67 0.8676 5.678 3.258
171 11.41 12.95 0.8560 5.090 2.775
185 12.11 13.27 0.8639 5.236 2.975
39 13.50 13.85 0.8852 5.351 3.158
76 16.53 15.34 0.8823 5.875 3.467
91 16.87 15.65 0.8648 6.139 3.463
35 17.08 15.38 0.9079 5.832 3.683
121 18.65 16.41 0.8698 6.285 3.594
169 11.48 13.05 0.8473 5.180 2.758
162 11.35 13.12 0.8291 5.176 2.668
46 14.79 14.52 0.8819 5.545 3.291
173 12.19 13.36 0.8579 5.240 2.909
189 12.62 13.67 0.8481 5.410 2.911
7 16.63 15.46 0.8747 6.053 3.465
26 12.74 13.67 0.8564 5.395 2.956
148 11.36 13.05 0.8382 5.175 2.755
58 11.23 12.63 0.8840 4.902 2.879
72 17.32 15.91 0.8599 6.064 3.403
103 19.94 16.92 0.8752 6.675 3.763
198 12.30 13.34 0.8684 5.243 2.974
56 15.38 14.77 0.8857 5.662 3.419
184 10.82 12.83 0.8256 5.180 2.630
Asymmetry.Coeff Kernel.Groove
59 3.220 4.605
5 2.462 4.956
20 2.688 5.219
124 5.366 5.661
52 1.481 5.487
19 3.072 5.176
161 3.638 5.338
55 1.142 5.088
69 2.936 6.079
2 2.699 4.825
98 4.308 6.009
10 1.717 5.001
75 2.858 5.746
134 5.304 5.395
193 3.919 5.001
63 1.313 5.150
110 2.248 6.163
78 5.173 6.187
178 4.179 4.956
114 3.063 6.320
149 5.813 5.219
129 4.972 5.847
61 1.176 4.782
87 3.120 6.053
102 3.747 5.929
120 4.188 5.992
168 4.702 4.963
1 1.018 4.956
47 2.129 5.351
171 4.957 4.825
185 4.132 5.012
39 2.249 5.176
76 5.532 5.880
91 3.696 5.967
35 2.956 5.484
121 4.391 6.102
169 5.876 5.002
162 4.337 5.132
46 2.704 5.111
173 4.857 5.158
189 3.306 5.231
7 2.040 5.877
26 2.504 4.869
148 4.048 5.263
58 2.269 4.703
72 3.824 5.922
103 3.252 6.550
198 5.637 5.063
56 1.999 5.222
184 4.853 5.089
# Training SVM classifier and Tuning hyperparameters using GridsearchCV
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
#--- define parameters set using dictionary
param = { "C" : [1.0, 10, 100, 100] , "gamma" : [1, 0.1, 0.01, 0.001, 10], "kernel" : ["rbf"]}
grid = GridSearchCV(SVC(), param_grid= param, refit= True, verbose= 3)
grid.fit(X_train, y_train)
# best grid search param
best_param = grid.best_params_
print(best_param)
{'C': 100, 'gamma': 0.1, 'kernel': 'rbf'}
grid_prediction = grid.predict(X_test)
grid_prediction
# report
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, grid_prediction))
print("===============================")
print(classification_report(y_test, grid_prediction))
[[18 1 0]
[ 0 16 0]
[ 0 0 15]]
===============================
precision recall f1-score support
1 1.00 0.95 0.97 19
2 0.94 1.00 0.97 16
3 1.00 1.00 1.00 15
accuracy 0.98 50
macro avg 0.98 0.98 0.98 50
weighted avg 0.98 0.98 0.98 50
